Artificial intelligence for solving physics problems

Artificial Intelligence (AI) is beginning to impact science, like physics, by solving some of the most complex, time-consuming, or even impossible problems humans solve. This post discusses some of the applications of artificial intelligence in physics that have been extensively researched. Physicists are also tasked with deciphering deep learning. Deep neural networks are being used in a growing number of applications for automated learning from data, but core theoretical questions regarding how they function remain unanswered. A physics-based solution may assist in closing the gap.

Here’s where physics comes into play:

To explain the situation to a scientific audience, one might equate the present state of deep learning theory to the early twentieth-century physics theory of light and matter. For example, many experimental effects (such as the photoelectric effect) could not be interpreted by the current theory because quantum mechanics had not yet been established. Theoretical physics science, in particular, is heavily reliant on models. Models are a means of catching the nature of a dilemma while excluding the information that isn’t needed to clarify experimental findings. The commonly used Ising model of magnetism is an example: it does not catch some specifics of the quantum mechanical aspects of magnetic interactions, nor does it include any details of any particular magnetic substance, but it describes the nature of the transformation from a ferromagnet to a paramagnet at high temperature [1].

More than three decades ago, physicists, especially those studying statistical dynamics of disordered systems, realised the need for machine-learning system modelling. A dynamical system with several interacting elements (weights of the network) emerging in organised quenched disorder is studied from a physics perspective (given by the data and the data-dependent network architecture) [2].

1. A Machine Learning Approach for Solving the Heat Transfer Equation Based on Physics

In manufacturing and engineering applications where parts are heated in ovens, a physics-based neural network is designed to solve conductive heat transfer partial differential equations (PDEs) as boundary conditions (BCs), as well as convective heat transfer PDEs. New research methods based on trial and error finite element (FE) simulations are inefficient since convective coefficients are always uncertain. The loss function is represented using errors to satisfy PDE, BCs, and the initial state. Loss words are reduced simultaneously using an integrated normalising scheme. Function engineering also employs heat transfer theory. Through comparing 1D and 2D predictions to FE outcomes, the predictions for 1D and 2D cases are verified. Heat transfer outside the training zone can be predicted using engineered elements, as seen. The trained model enables rapid measurement of various BCs to create feedback loops, bringing the Industry 4.0 idea of active production management based on sensor data closer to reality. A first layer for the neural network was created by merging two pre-layers of words, as seen in Figure 1 [3], to incorporate function engineering.

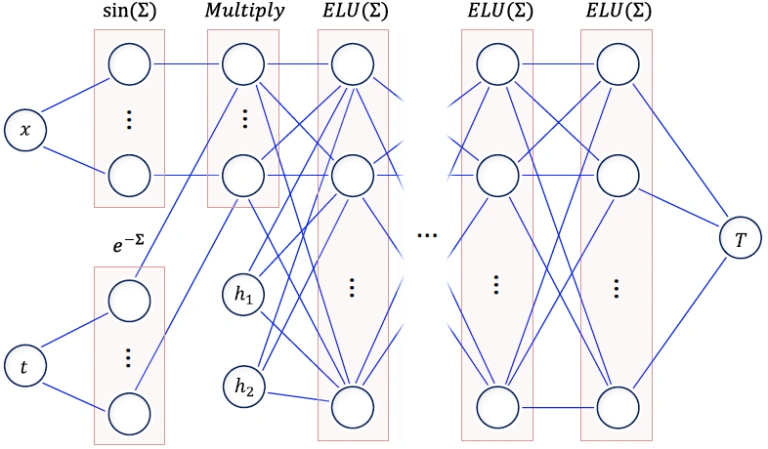
Figure 1: A neural network with physics-infirmed engineered features is seen in a schematic to solve the heat transfer PDE [3].

2. Deep Learning Method for Solving Fluid Flow Problems

The Physical Informed Neural Network (PINN) is used in conjunction with Resnet blocks to solve fluid flow problems based on partial differential equations (i.e., the Navier- Stokes equation) embedded in the deep neural network’s loss function. The initial and boundary parameters are both considered in the loss function. Burger’s equation with a discontinuous solution and Navier-Stokes (N-S) equation with a continuous solution was chosen to verify the efficiency of the PINN with Resnet blocks. The findings show that the PINN with Resnet blocks (Res-PINN) outperforms conventional deep learning approaches in terms of predictive ability. Furthermore, the Res-PINN can predict the whole velocity and pressure fields of spatial-temporal fluid flow, with a mean square error of 10^-5. The streamflow inverse problems are also well-studied. In clean data, the inverse parameters have errors of 0.98 % and 3.1 %, respectively, and in noisy data, they have errors of 0.99 % and 3.1 %. A schematic diagram of a physics-informed neural network used to solve a fluid dynamics model is seen in Figure 2 [4].

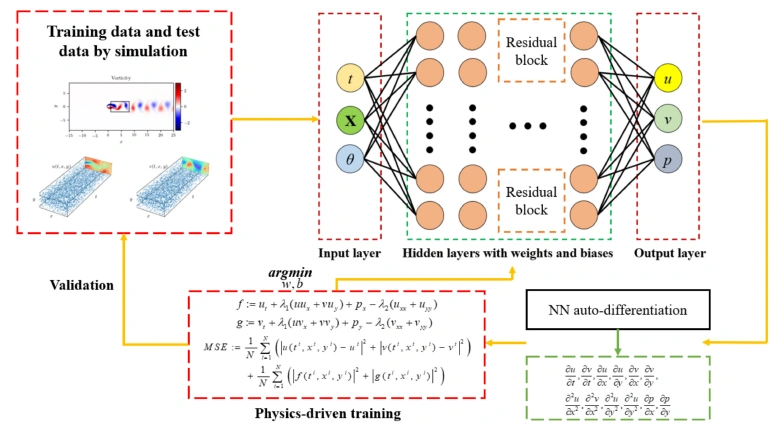
Figure 2. A diagram of the physical informed neural network used to solve the fluid dynamics model  [4].

Interesting blog: Difference Between Artificial Intelligence And Machine Learning?

3. Kohn-Sham Equations as Regularizer – A Machine Learned Physics

Machine learning (ML) techniques have sparked a lot of interest to boost DFT approximations. The implied regularisation provided by solving the Kohn-Sham equations with training neural networks for the exchange-correlation functional improves generalisation. Two separations are enough to learn the entire one-dimensional H2 dissociation curve, including the highly correlated field, with chemical precision. Our models also transcend self-interaction error and generalise to previously unseen forms of molecules. The KS-DFT is depicted in Figure 3 as a differentiable programme [5].

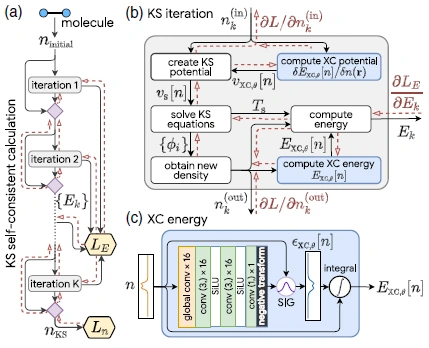
FIG. 3. KS-DFT as a differentiable program [5].

4. Machine Learning for Quantum Mechanics

Quantum information technology and intelligent learning systems, on the one hand, are both emerging technologies with the potential to change our culture in the future. Quantum knowledge (QI) versus machine learning and artificial intelligence  (AI) are two underlying areas of basic science that both have their own set of questions and challenges. Using machine learning algorithms, pairF-Net, a modern chemically intuitive method, precisely predicts the atomic forces in a molecule to quantum chemistry precision. A residual artificial neural network was developed and trained with features and objectives focused on pairwise interatomic forces to determine the Cartesian atomic forces suitable for molecular mechanics and dynamics calculations. The scheme predicts Cartesian forces as a linear combination of a series of force components on an interatomic basis while maintaining rotational and translational invariance implicitly. The system will estimate the reconstructed Cartesian atomic forces for a set of small organic molecules to less than 2 kcal mol^-1 Å^-1 using reference force values obtained from density functional theory.  The pairF-Net scheme uses a simple and chemically understandable route to have atomic forces at a quantum mechanical level at a fraction of the cost, paving the way for effective thermodynamic property calculations. The artificial neural network architecture is depicted in Figure 4 [6].

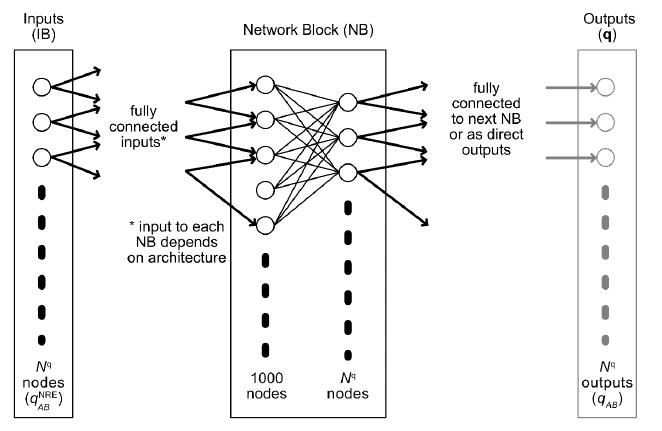
Figure 4.  Artificial neural network architecture: General arrangement of layers, network blocks (NBs), and connectivity for input block (IB), NBs, and output layer [6].

Conclusion

While AI has aided many advances in physics, physics still aids AI methods in various ways. Quantum machines, for example, are based on the fundamental laws of quantum mechanics. Many AI approaches have been derived from basic physics laws. Both kinds of research complement each other most significantly, benefiting humanity to achieve newer and more comprehensive breakthroughs in Science and Technology. Let us, as physicists, welcome machine learning as a modern method in our toolbox, and use it broadly and wisely. But bear in mind that learning why and how it works necessitates physics methodology, so we shouldn’t sit back and watch this massive undertaking unfold. So let us welcome deep neural networks into our field and research them with the same zeal that fuels our search to comprehend the world around us.

Tutors India Helps Can  help you in the Artificial Intelligence and Machine learning project writing Help for students Our Subject mater expertise can Bridge the AI Skills Gap & help you to get your professional academic degree.

Reference:

[1] Zdeborová, L. Understanding deep learning is also a job for physicists. Nat. Phys. 16, 602–604 (2020).

Muhammad Aurangzeb Ahmad and Şener Özönder. 2020. Physics Inspired Models in Artificial Intelligence. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD ’20). Association for Computing Machinery, New York, NY, USA, 3535–3536. DOI:

1. Navid Zobeiry, Keith D. Humfeld, A physics-informed machine learning approach for solving heat transfer equation in advanced manufacturing and engineering applications, Engineering Applications of Artificial Intelligence, Volume 101, 2021, 104232,.

2. Cheng, C.; Zhang, G.-T. Deep Learning Method Based on Physics Informed Neural Network with Resnet Block for Solving Fluid Flow Problems.  Water 2021, 13, 423..

3. Li, Li and Hoyer, Stephan and Pederson, Ryan and Sun, Ruoxi and Cubuk, Ekin D. and Riley, Patrick and Burke, Kieron, Kohn-Sham Equations as Regularizer: Building Prior Knowledge into Machine-Learned Physics, Phys. Rev. Lett., 126, 2021, 036401. 10.1103/PhysRevLett.126.036401.

6. Ramzan, Ismaeel; Kong, Linghan; Bryce, Richard; Burton, Neil (2021): Machine Learning of Atomic Forces from Quantum Mechanics: a Model Based on Pairwise Interatomic Forces. ChemRxiv.Preprint.